Just how big is it?

[Detonate]

Yes, I have seen folks ponder on this question for hours without coming up with the correct answer when it is a simple Distance, Time, Rate problem. He must complete the two laps in two minutes to average 60 mph. He already used the two minutes on the first lap.

[HalationEffect]

More fun with numbers: 0.999... = 1. (Zero point nine nine nine recurring equals one).

Not just practically the same, or so close as makes no difference; they are the same number. Getting to grips with that idea really curdled my grey matter for a while!

[Qqmike]

"they are the same number. " -- Well, only in the sense that the infinite series of summations of negative powers of ten CONVERGES to 1 (i.e., 1 is the limit of the series), using the real number system as a "field." But, of course, in a number theoretic sense, or set theoretic sense, or ring theoretic sense, for example, the number "1" (so-called) is another animal. Right?

[Snowhog]

0.999...

In mathematics, the repeating decimal0.999... (sometimes written with more or fewer 9s before the final ellipsis, or as 0.9, 0.(9), or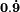 ) denotes a real number that can be shown to be the number one. In other words, the symbols "0.999..." and "1" represent the same number. Proofs of this equality have been formulated with varying degrees of mathematical rigor, taking into account preferred development of the real numbers, background assumptions, historical context, and target audience.Every nonzero, terminating decimal has an equal twin representation with trailing 9s, such as 8.32 and 8.31999... The terminating decimal representation is almost always preferred, contributing to the misconception that it is the only representation. The same phenomenon occurs in all other bases or in any similar representation of the real numbers.
The equality of 0.999... and 1 is closely related to the absence of nonzero infinitesimals in the real number system, the most commonly used system in mathematical analysis. Some alternative number systems, such as the hyperreals, do contain nonzero infinitesimals. In most such number systems, the standard interpretation of the expression 0.999... makes it equal to 1, but in some of these number systems, the symbol "0.999..." admits other interpretations that contain infinitely many 9s while falling infinitesimally short of 1.
The equality 0.999... = 1 has long been accepted by mathematicians and is part of general mathematical education. Nonetheless, some students find it sufficiently counterintuitive that they question or reject it, commonly enough that the difficulty of convincing them of the validity of this identity has been the subject of numerous studies in mathematics education.

[HalationEffect]

"they are the same number. " -- Well, only in the sense that the infinite series of summations of negative powers of ten CONVERGES to 1 (i.e., 1 is the limit of the series), using the real number system as a "field." But, of course, in a number theoretic sense, or set theoretic sense, or ring theoretic sense, for example, the number "1" (so-called) is another animal. Right?

Just follow the link Snowhog posted to see that there are several formal mathematical proofs that they're the same number.

[Qqmike]

Uh, well ... It's a matter of words, terminology.
0.99999.... = 1 in the sense that the left side converges to the right side; or even more precisely, the limit of the series represented by the left side is equal to "1." Limit, as in mathematical limit, as in arbitrarily close, as in "choose any arbitrary epsilon positive," and you can show that a member of the series on the left is within epsilon of the right. And so on. I know what you guys mean to say, colloquially, but I'm not sure you know what I'm trying to say. I am making precise what you mean to say! The left is not equal to the right but only in the sense that the infinite series represented by the left converges in the real number field to the number 1. There, that's better.
http://en.wikipedia.org/wiki/Limit_%28mathematics%29
I'm not picking at straws, I'm, just trying to be precise.
If, for example, you focus ONLY on the ring of positive integers embedded in the real field, then what?! There is not such thing as 0.9999...., and so then what is "1"? (1, viewed "as itself," as a positive integer, etc.)

[Qqmike]

This might help.
0.9999 means
9*(10^(-1) + 10^(-2) + 10^(-3) + ... )
and that infinite summation equals (in the sense that the partial, finite sums converges to) "1" (as the number of summands approaches infinity). None of this makes any sense unless you do have a field, in this case the real field (with multiplicative identity and inverses and so on). All of this is true for any base (here, the base is 10).

[HalationEffect]

Another way of looking at it - The set of real numbers is subject to the Archimedean property (that there are no non-zero infinitesimals; i.e. all infinitesimals are equal to zero), therefore saying that the difference between 0.999... and 1 is infinitesimal is the same thing as saying the difference between them is zero.

But for me, the best proof is the simplest, and the Wikipedia page has it:

One ninth (1/9) expressed as a decimal is 0.111...
0.111... x 9 = 0.999...
But axiomatically, one ninth multiplied by nine *must* equal one, right?

[bsniadajewski]

Yes, I have seen folks ponder on this question for hours without coming up with the correct answer when it is a simple Distance, Time, Rate problem. He must complete the two laps in two minutes to average 60 mph. He already used the two minutes on the first lap.

Yeah, tyhat problem had me thinking about it for a bit. At first I thought "90 MPH" due to averages ((30+90)/2 = 60), but then I read this then I said "Ahhh, I see".

[Qqmike]

"One ninth (1/9) expressed as a decimal is 0.111...
0.111... x 9 = 0.999..."

Only in the sense of convergence of infinite series (convergence of the series of finite summations as the number of summands approaches infinity). See my post #22 above. I think we mean the same things here, I'm just making it mathematically precise. It is not an axiom that 9 times one-ninth equals 1. Strictly speaking, for the number 9 in the real field, by the axioms of a field (the real field in this case), there * exists * a multiplicative inverse, and we agree to denote that inverse by, say, 1/9 or 9^(-1), but we could agree to denote it by anything, 9^*, egg9, z9, 9z, whatever.

[HalationEffect]

For a good explanation (better than Wikipedia's IMO) of why limits and arbitrary closeness don't disprove that 0.999... = 1, see: http://www.purplemath.com/modules/howcan1.htm

Especially the last section "Argument from semantics", which, as far as I can tell, outlines the objection you're raising.

A common objection is that, while 0.999... "gets arbitrarily close" to 1, it is never actually equal to 1. But what is meant by "gets arbitrarily close"? It's not like the number is moving at all; it is what it is, and it just sits there, looking at you. It doesn't "come" or "go" or "move" or "get close" to anything.

On the other hand, the terms of the associated sequence, 0.9, 0.99, 0.999, 0.9999, ..., do "get arbitrarily close" to 1, in the sense that, for each term in the progression, the difference between that term and 1 gets smaller and smaller. No matter how small you want that difference to be, I can find a term where the difference is even smaller.

This "getting arbitrarily close" process refers to something called "limits". You'll learn about limits later, probably in calculus. And, according to limit theory, "getting arbitrarily close" means that they're equal: 0.999... does indeed equal 1.

Emphasis mine.

Yeah, we probably do mean the same thing, and are just expressing it differently. It's been almost 30 years since I had to study any maths beyond high school level, and I've forgotten most of it.

[Qqmike]

"No matter how small you want that difference to be, I can find a term where the difference is even smaller."

That's my epsilon in Post #21.

I think what you guys are wrestling with--or addressing--is how we humans can understand the notion of mathematical limit, and that's why I linked in post #21 to
http://en.wikipedia.org/wiki/Limit_%28mathematics%29

To beginning students of math, the notion of limit is confusing, or difficult to grasp, it's the first step in understanding differential calculus. It helps to actually write down an arbitrarily small positive real number epsilon (like 1/1000000000000) and then as an exercise actually produce the partial, finite summation that is within that epsilon of the number 1; and then to pick an even small epsilon and do it again, if necessary, until one becomes convinced.

0.9999 does not actually equal 1. ONLY in the sense that 0.999 is shorthand notation for an infinite series (of finite partial summations) that converges in the real number field to the real number 1.

I really mean no offense here, but I think I've said it about as well as most mathematicians could (is there another mathematician here who could pitch in?), and so I'll step back for now and let you mull this over. I can't tell you how many calculus classes I have taught at the master's level.

[Qqmike]

Yes, HalationEffect, me, too, I'm 64 and haven't done this work since about 1987 or so; although every now and then, a neighbor or a relative drags me back into it. Yes, I think we are on the same page. My bent is * pure * math, and so that sort of makes me, a priori, kind of an a*hole in how I communicate sometimes as I insist upon clinically clean rigor! ;-)

[SteveRiley]

I car goes around a circular one mile track, on the first lap the driver averages 30 MPH. How fast will he have to drive the second lap to average 60 mph for both laps?

I've seen this one before, including all the various debates. Here's how it was explained to me...

People who arrive at 90 mph for the second lap are led to this mistake in two ways: they don't realize that time, not distance, matters, and they're blind to the fact that this is really a weighted average problem because the "weight" here is a distance of 1, making the divide-by-2 seem intuitive. The incorrect formula that people are shortcutting is:

           speed[SUB]1[/SUB] * distance[SUB]1[/SUB] + speed[SUB]2[/SUB] + distance[SUB]2[/SUB]
speed[SUB]avg[/SUB] = ---------------------------------------
                    distance[SUB]1[/SUB] + distance[SUB]2[/SUB]

Since what matters in this problem is the time, not the distance, the formula should instead be:

           speed[SUB]1[/SUB] * time[SUB]1[/SUB] + speed[SUB]2[/SUB] + time[SUB]2[/SUB]
speed[SUB]avg[/SUB] = -------------------------------
                    time[SUB]1[/SUB] + time[SUB]2[/SUB]

How to know that the weight is time? Look at the phrasing of the question: specifically, which denominator is used. Here it's hour. Thus, time.

http://gmatclub.com/forum/a-certain-...-a-127918.html

Qqmike: seems reasonable, would you agree?

[Qqmike]

S-R, Post #29: Yes, I think ;-)

I've never been good at practical, word, math problems, and was surrounded by practical engineers and scientists in undergrad college who were (Rose Polytechnic Inst of Technology, now called Rose-Hulman Inst of Tech). As I say, a pure math guy here.

But here, yes, miles per hour --> miles/hour => distance divided by time. Your formula looks right. 30 mph takes 1/30 of an hour to cover 1 mile (speed1*time1); ditto for speed2*time2.
Not being good at this sort of thing, I can only get at it naively, x being the unknown speed to solve for:

mph must be 60

miles/hour must be 60

(1+1)/((1/30) + (1/x)) = 60
which reduces to 1/30 + 1/x = 1/30, and so implies x --> infinity (so 1/x --> 0).

That equation--and the thinking behind it--comes down what you are saying and your equation, Steve, right?

Sorry about my lack of typesetting skills for math symbols.

(I'll check back here later or in the morning, got some family urgency/emergency brewing long distance this evening.)